
|
|
|||||
|
Foro: * Dinámica * Autor: Blackgirl Resptas: 5 |
Foro: * Dinámica * Autor: Mabyy Resptas: 1 |
Foro: * Dinámica * Autor: Blackgirl Resptas: 3 |
Foro: * Dinámica * Autor: Wouvell Resptas: 3 |
|
|
|
 
|



|
Página 1 de 1
|
| Autor | Mensaje | ||||
|---|---|---|---|---|---|
|
|||||
|
|
|
||||
|
|
|||||
|
|
|||||
|
|||||
|
|
|
||||
|
|
|||||
|
|||||
|
|
|
||||
|
|
|||||
|
|
|||||
 
|



|
Página 1 de 1
|
|
||||||
|
|






 Vistas: 10706
|
Vistas: 10706
|  Favoritos: 0
|
Favoritos: 0
|  Suscritos: 5
Suscritos: 5 
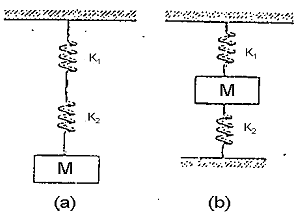 Los módulos de elasticidad de los resortes en la figura son, respectivamente k1 y k2. Calcular la constante k del sistema cuando los dos resortes están conectados como en (a) y (b)
Los módulos de elasticidad de los resortes en la figura son, respectivamente k1 y k2. Calcular la constante k del sistema cuando los dos resortes están conectados como en (a) y (b)


