|
|
![]()
![]()
 |
| Si se te ocurre alguna pregunta, planteala en el foro de física. ==> FORO-FIS | |
| ¿Qué piedra llega antes al suelo? | |
|
Una
piedra tiene una masa dos veces mayor que otra. Sus volúmenes son
parecidos (densidad doble). Se las deja caer desde un acantilado,
¿cuál llegará antes al suelo? ¿Cuál tendrá más velocidad?. Sabemos que si queremos
empujar a dos ciclistas, uno con doble masa que el otro (incluida la
bici), para que fueran acelerando a la par, tendríamos que empujar
con una fuerza doble al que tiene doble masa. Es normal pues, en
realidad, al que tiene masa "dos" se le puede
considerar como dos cuerpos de masa "uno". De esta forma
ambos terminarían su recorrido en el mismo tiempo y con la misma
velocidad. Para que dos piedras de masas distintas (una doble que la
otra) lleguen al suelo al mismo tiempo y con la misma velocidad habrá
que empujarlas, hacia abajo, con una fuerza doble a la que tiene doble
masa. Esto es precisamente lo que hace la Tierra. Al ser el peso
proporcional a la masa (Peso = masa · gravedad), la piedra con doble
masa pesa el doble. En consecuencia ambas llegan al suelo
simultáneamente y con la misma velocidad. Sin embargo, la energía de
la primera es doble ya que la energía cinética es proporcional a la
masa y al cuadrado de su velocidad. La velocidad de ambas es la misma
pero su masa no. |
|
| ¿Se puede escapar de la gravedad de la Tierra? | |
 |
La única manera de escapar de la gravedad de la Tierra es situándonos en su centro. De esta manera, ésta, nos atraerá en todas las direcciones y se compensarán estas atracciones entre sí. Esto no sería posible en la realidad ya que, debido a que está en pleno proceso de enfriamiento, su centro es líquido (materiales fundido). |
| ¿Cuánto de lejos debemos situarnos para que no pesemos? | |
 |
Un matemático diría que en el infinito. Esto quiere decir que en ningún sitio. Mientras más lejos estemos menos pesamos pero nunca valdrá cero. También es verdad que, para por ejemplo una piedra, la atracción gravitatoria se puede considerar casi nula a varios metros de ella. Matemáticamente cuando R tiende a infinito F tiende a cero pero no hay ningún valor de R que haga que F sea cero. |
| ¿Por qué la Luna no cae como la manzana? | |
| En realidad la Luna cae aproximadamente 0,125 cm cada segundo. Mientras la Luna cae la Tierra se va curvando con la misma rapidez con que lo hace la trayectoria de la Luna. La Luna, debido a su inercia, tiende a alejarse de la Tierra según una línea recta cuya dirección viene dada por su velocidad. El planeta, por otro lado, la atrae debido al peso del satélite. Ambos efectos se contrarrestan. La Luna no se va por la tangente y la Tierra no puede hacer que impacte sobre ella. Se dice, entonces, que el satélite está en órbita. Casi idéntico a cuando hacemos girar una piedra atada a una cuerda alrededor nuestro. Ahora, es la cuerda la que mantiene la masa a igual distancia de la mano pues, al tensarse, tira de la piedra hacia el centro de giro. | |
|
¿Es
grande la fuerza de atracción gravitatoria?
Ma · Mb F = G · ————— R2ab |
|
|
6,67 · 10-11 N·m2/Kg2 G GRAVITACIÓN UNIVERSAL NEWTON ¿Cómo funciona la gravedad?
|
¿Por qué en torno nuestro no se manifiesta constantemente, en las circunstancias
normales, la ley
de la atracción universal? ¿Por qué no vemos cómo se atraen entre sí las mesas, las sandías, las personas? Porque
cuando los objetos son pequeños la fuerza de atracción que ejercen es muy pequeña. Citaré un ejemplo ilustrativo.
Dos personas que se encuentren a dos metros de distancia entre sí se atraen mutuamente, pero la fuerza de esta
atracción es insignificante. Suponiendo que estas dos personas tienen un peso medio, la atracción será de 1 /100 de
miligramo. Esto quiere decir que estas dos personas se atraen mutuamente con la misma fuerza con que una pesita
de 1/100 000 de gramo presiona sobre el platillo de una balanza. Solamente las balanzas de extraordinaria
sensibilidad de los laboratorios de investigación pueden apreciar un peso tan insignificante. Claro está que esta
fuerza no puede hacer que nos movamos del sitio, puesto que lo impide el rozamiento entre las suelas de nuestros
zapatos y el suelo. Para que nos movamos, estando sobre un suelo de madera, por ejemplo (la fuerza de rozamiento
entre las suelas de los zapatos y el suelo será en este caso igual al 30% del peso de nuestro cuerpo), hace falta que
sobre nosotros actúe una fuerza mínima de 20 Kg. Resulta cómico comparar esta fuerza con la de una centésima de
miligramo, que es la que ejerce la atracción. Un miligramo es la milésima parte de un gramo, y un gramo es la
milésima parte de un kilogramo; por lo tanto, 0,01 mg será... ¡la mitad de la mil millonésima parte de la fuerza
necesaria para hacer que nos movamos del sitio! Siendo así, ¿qué tiene de particular que, en condiciones normales,
no nos demos ni la más leve cuenta de la atracción entre los cuerpos terrestres? Si no existiera el rozamiento seria otra cosa; entonces nada impediría que hasta la más leve atracción provocara la aproximación de los cuerpos entre sí . Pero en este caso la aproximación mutua de dos personas producida por una fuerza de atracción de 0,01 mg sería también muy lenta, es decir se realizaría con una velocidad insignificante. Por medio de cálculos se puede demostrar que, si no existiera rozamiento, dos personas situadas a 2 m de distancia se aproximarían entre sí (por influjo de la atracción mutua) 3 cm durante la primera hora, 9 cm durante la segunda y 15 cm durante la tercera. El movimiento de aproximación se iría acelerando, pero las dos personas no llegarían a juntarse antes de cinco horas. La atracción entre los cuerpos terrestres se puede notar en aquellos casos en que la fuerza de rozamiento no es un obstáculo, es decir, cuando los cuerpos no se mueven. Un peso colgado de un hilo se halla sometido a la atracción de la Tierra (por eso el hilo está dirigido verticalmente), pero si cerca de este peso se encuentra un cuerpo cuya masa sea grande, aquél será atraído por éste y el hilo se desviará ligeramente de su posición vertical y tomará la dirección de la resultante entre la atracción de la Tierra y la del cuerpo, que será relativamente muy pequeña. La desviación de una plomada en las proximidades de una gran montaña fue observada por vez primera en el año 1775 en Escocia, por Maskelyne, quien comparó la dirección de dicha plomada con la del polo celeste, por los dos lados de una misma montaña. Posteriormente se realizaron otros experimentos más perfectos, utilizando balanzas especiales, que permitieron determinar exactamente la fuerza de la atracción. Como hemos visto, la fuerza de la atracción entre masas pequeñas es insignificante. A medida que aumenten las masas crece la atracción proporcionalmente al producto de éstas. |
| ¿Es posible lanzar un objeto hacia arriba y que no regrese a Tierra? | |
| Efectivamente. Todo cuerpo situado en la superficie de un planeta está ligado a él por una energía negativa (de atracción) llamada energía potencial gravitatoria. Para que escape habrá de comunicársele una velocidad determinada para que su energía cinética (de movimiento) compense la atractiva. Es por ello que podemos lanzar naves espaciales que, ahora, están viajando hacia fuera de nuestro sistema solar. La velocidad de escape para la Tierra es, aproximadamente, de 11 Km/s. (ver fórmulas). | |
| ¿Realmente gira la Luna alrededor de la Tierra? | |
| No. Entre la Tierra y la Luna hay un punto llamado centro de masa (es una especie de "resumen" de las masas de ambos astros). Este punto está más cerca del planeta (casi en su superficie) ; ambos giran alrededor de dicho punto. Es decir, ambos realizan un movimiento circular alrededor del centro masa (con radios diferentes). Para entenderlo mejor, supongamos que tuvieran masas iguales ¿porqué iba a estar uno, en el centro, girando alrededor del Sol, y el otro haciendolo alrededor de la Tierra?. En este caso el centro de masas estaría entre los dos cuerpos y sería éste el que orbitaría alrededor del Sol. | |
|
¿Por
qué se ve siempre la misma cara de la Luna? (En la imagen tienes la cara que nunca se ve desde la Tierra) |
|
 |
Siéntate en una silla que sea giratoria y extiende tu brazo delante de la cara, con el puño mirando hacia ti; comienza a girar sin perder de vista tu puño, dando vueltas. ¿Verás el lado opuesto de tu puño en algún momento, mientras giras?. La respuesta es, evidentemente, que no, pues mientras tu cabeza ha dado una vuelta en un cierto tiempo, tu puño ha realizado el mismo giro en el mismo tiempo. Si te fijas en el movimiento de tu mano, veras que una de sus caras se enfrenta a cada una de las cuatro paredes de la habitación, igual que la cabeza, por lo tanto, ambos giran con la misma velocidad angular (recorren ángulos iguales en tiempos iguales). |
| ¿Se puede colocar un satélite artificial que esté siempre encima de nuestro país? | |
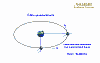 |
Para colocar un satélite artificial en órbita, debemos conocer la distancia al planeta pues la velocidad que tendremos que darle dependerá de lo cerca o lejos que esté de él. Es decir, no podemos elegir ambas magnitudes (distancia y velocidad). En el caso que nos ocupa, la velocidad angular del artificio deberá ser la misma que la de la Tierra (una vuelta por día), lo que nos permite calcular la posición donde, aparentemente, esté en reposo, encima de nuestras cabezas. Esa distancia es de, aproximadamente, 36.000 Km desde la superficie del planeta. Esta órbita recibe el nombre de geoestacionaria porque parece estar quieto respecto de la Tierra. |
| ¿Qué es la velocidad angular y el radián? | |
 ω=∆φ/t |
Cuando algo gira, lo hace alrededor de un punto. Un tiovivo nos puede servir de ejemplo. Situémosno en el centro y observemos un caballito que se encuentra a una distancia R. Veremos que describe una circunferencia con ese radio. Hagamos girar el carrusel de manera que el caballito recorra linealmente una distancia igual a la que le separa del centro R. Visto desde el centro, una línea trazada desde él hasta el objeto, barre un ángulo llamado radián. Pero este ángulo o la distancia que debe moverse ,R, el cuadrúpedo puede hacerse muy despacio o muy rápido . Cuando ese tiempo es de un segundo, se dice que tiene una velocidad angular de un radián/segundo. La velocidad angular es el ángulo (medido en radianes) que barre el caballito en un segundo. Se representa con la letra w y gráficamente se expresa con un vector perpendicular al plano de giro. |
| ¿Qué ocurriría si aumentase o disminuyese la velocidad de la Luna? | |
 |
Se podría pensar que la Luna está en un equilíbrio inestable en su orbita, es decir, que si aumentamos o disminuimos la velocidad de ésta, se saldrá de su trayectoria y la perderíamos o nos estrellaríamos contra ella. Siempre que la variación de la velocidad no sea extremadamente grande, el satélite modificará la trayectoria que ahora será más achatada, elíptica, pero permanecería girando alrededor de la Tierra. En el supuesto concreto de disminuir su impulso, pasaría más cerca y las mareas marinas serían mucho más problemáticas. |
| ¿A qué velocidad se mueve la gravedad? | |
|
La velocidad de la "gravedad"
c 300 000 km/s
Las leyes de Newton no predicen esa velocidad, las de Einstein sí. |
Hecha la pregunta así, suena un poco raro. La palabra gravedad nos trae a la imaginación cuerpos atrayéndose por la acción de las masas; ¿cómo se puede mover eso?. Si estuvieras tu solito en el Universo tu cuerpo no tendería a acelerar en ninguna dirección (no he dicho moverse) pero si hubiera otro cuerpo, acompañándote, entonces te acelerarías en su dirección, hacia si. (si ese otro cuerpo fuera la Tierra, a esa atracción la llamaríamos peso). Hagamos el siguiente experimento: En principio, tu eres el único cuerpo que existe. En un instante determinado aparece la Tierra (de repente), a una distancia D (conocida). Si medimos el tiempo que pasa desde que apareció la Tierra hasta que tú empezastes a acelerar en dirección al planeta, dividiendo ambas magnitudes nos daría la velocidad a la que se mueve la gravedad (la atracción entre masas). Esta experiencia no es realizable, tal como la hemos planteado aquí. ¿Que podemos hacer entonces para conocer la velocidad en cuestión? Recurrir a las leyes matemáticas para ver que predicen o preguntar al creador de la teoría. Para Newton y su modelo, la atracción entre cuerpos es instantánea (velocidad infinita). Para Einstein, la velocidad de esa atracción es la de la luz, c. Hay que tener en cuenta que en la "Teoría de la Relatividad" (la pongo entre comillas porque ya es una ley empírica como lo fue la de Newton), los cuerpos no se atraen porque lo hagan sus masas, sino porque curvan el espacio (lo explicaremos en otra ocasión). Era una pregunta difícil que Einstein supo resolver. Por eso ya no son válidas las leyes de la Física Clásica, porque no responden bien ante preguntas como esta. |
|
|