|
|
|
CAMPO GRAVITATORIO |
||
| Ley de Newton (gravitación Universal) |
 |
G : cte gravitación Universal G = 6,67·10-11 N·m2/Kg2 ur = r / |r| vector unitario radial |
| Fuerzas que un sistema de masas puntuales (Mi) ejerce sobre otra masa puntual (M) |
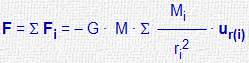 |
ri = vector de mi a m ≠ 0 ur(i) = vector unitario de mi a m |
| Fuerza ejercida por una distribución continua de masa |
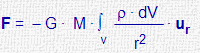 |
r = densidad de materia V: volumen |
| Campo gravitatorio terrestre en su superficie |
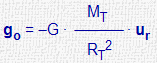 |
go : gravedad en RT = 9,81 N/Kg G·MT = go·RT2 |
|
INTENSIDAD CAMPO GRAVITATORIO |
POTENCIAL GRAVITATORIO |
|
| Masa aislada (M1) |
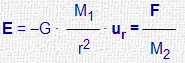 |
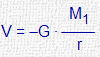 |
| Sistema de masas puntuales |
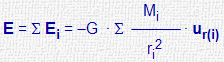 |
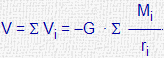 |
| Distribución continua de masas |
|
|
| Capa esférica de radio R | ||
| En el interior (r<R) | E = 0 |
|
| En la superficie (r=R) |
|
|
| En el exterior (r>R) |
|
|
| Esfera uniforme de radio R | ||
| En el interior (r<R) |
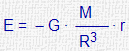 |
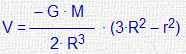 |
| En la superficie (r=R) |
|
|
| En el exterior (r>R) |
|
|
|
LEYES DE KEPLER |
||
| Primera ley | Los planetas describen órbitas elípticas alrededor del Sol, encontrándose éste en uno de sus focos. | |
| Segunda ley | Los radiosvectores que describen la posición del planeta desde el Sol, barren áreas iguales en tiempos iguales. Su velocidad aerolar es cte. (Principio de conservación del momento cinético. L) | |
| Tercera ley |
T 2 —— = cte ; T2·G·M = 4·π2·R3 R3 |
T : periódo R : Semieje mayor de la elipse |
| Velocidad orbital | G·M vo2 = —— R |
R: Radio de la órbita |
| Velocidad escape |
2·G·M ve2 = ——— R |
ve2 = 2· vo2 |
| Relación entre el campo y el potencial |
E = - grad V E = - dV/dr |
V = - ∫ E · dr |