Ejercicios de matemáticas. Plano afín. 1. Galilei

PROBLEMAS Y CUESTIONES DE MATEMÁTICAS

PLANO AFÍN-EUCLÍDEO

	Determinar la ecuación de la recta, que pasa por el punto A(2,3) y tiene por vector director d(-1,4), en todas sus formas.
1
	Calcular la ecuación de la recta, en todas sus formas, que pasa por los puntos A(3,2) y B(-2,-2).
2
	Determinar la ecuación de la recta paralela a 3x - 2y + 5 = 0 que pase por el punto A(1,1)
3
	Determinar la ecuación de la recta perpendicular a la del ejercicio anterior y que pase por el punto A(2,-3)
4
	Calcular la ecuación de la recta, en todas sus formas, que pasa por el punto A(2,2) y A. Tiene por vector director d(1,0) B. " " " " d(0,1) C. " " " " d(1,1) D. " " " " d(-2,-2)
5
	Determinar a en la recta -X + 1 ----------- = Y - 2 a para que: A. Pase por el punto (2,-1) B. Sea paralela al vector d(1,-1) C. ¿Qué ocurre si a=0? D. Sea paralela a la recta de ecuación Y= 2 X + 1
6
	Dada la recta de ecuación: X = -2 + 2 k Y = -1 - 3 k A. ¿Pasa por el punto (0,-4)? ¿Cuál sería el valor correspondiente a k para ese punto? B. Obtener tres puntos distintos de esa recta. C. ¿Para qué valor de k se obtiene X=-2? ¿Qué ordenada (Y) corresponde a la abscisa X=-2? D. ¿Existe algún k para el cual X=Y? ¿A qué punto corresponde?
7
	Calcular la ecuación de la recta que pasa por el punto (1,-1) y que es paralela a la recta de ecuación 2 x + 4 y - 1 = 0.
8
	Determinar a en la ecuación a x + 2 y - 2 = 0 para que dicha recta sea paralela a la de ecuación: X - 1 Y + 2 -------- = -------- 2 -3
9
	Determinar el valor de a para que las dos rectas, r₁, r₂, r₃ y r₄ siguientes sean: A. paralelas B. perpendiculares C. formen un ángulo de 30º r₁ x = 2 - at ; y = 1 + t r₂ y = x r₃ 2a x - 3y = 1 r₄ 2y = 4x - 4
10
	Determinar los vectores directores y un punto de cada una de las rectas que se dan seguidamente: A. x = 2 - t ; y = -1 + 2t ; A.1. x = 1 - t ; y = -3t B. y = 3x + 2 ; B.1. x = 2y - 4 C. 2x + 3y - 1 = 0 ; C.1. 3y - 2x - 4 = 1 D. x y ; D.1. 3x 4y ----- + ----- = 1 --- - ---- = 2 2 3 2 3 E. (x,y) = (1,-2) + (2,2)t F. x - 2 y + 3 2x - 5 3y + 4 ------ = -------- ; F.1. --------- = - --------- 2 -3 2/3 1/5
11
	La ecuación de la paralela a x - 9 y ------------ = --------- 7 -8 y que pasa por el punto (-3,7).
12
	Determinar la ecuación de la recta, en forma explícita, que pasa por el punto medio del segmento definido por los puntos A(2,-5) y B(3,5)
13
	Representar las rectas, utilizando los valores dados, que se dan seguidamente: (d es el vector director) (t es el parámetro) A. P(-2,4) d(2,-3) ;; A.1. P(2,-3) d(2,0) B. Determinar las coordenadas de los puntos correspondientes al valor del parámetro, t, dado en ambas rectas: t = 0, 2, -3, -1, 1, 3/2, -5/3.
14
	Determinar las ecuaciones, en todas sus formas, de las rectas que pasan por los puntos dados seguidamente: A. A(2,-3) B(4,6) ;; A.1. A(-3,-5) B(2,4) B. A(3,3) B(3,-4) ;; B.1. A(3,3) B(-2,3)
15
	Calcular la ecuación de la recta, en todas sus formas, que pasa por el punto A(1,-2) y tiene por vector director d=3i-2j, siendo {i,j} una base de R².
16
	Dado el triángulo de vértices A(0,1), B(1,0) y C(0,0), calcular la ecuación de sus medianas.
17
	La recta r pasa por los puntos P(2,3) y Q(1,1). Hallar la ecuación de la recta s, tal que r sea paralela a s y el punto A(2,2) s.
18
	Sabiendo que se llama pendiente de una recta (m) a la tangente del ángulo que forma ella con el eje OX (positivo), es decir, m=d2/d1 = tg a ; determinar las pendientes de las siguientes rectas: A. 3 X + 4 Y - 5 = 0 B. Y = 2 X + 1 C. X= 2 + k ; Y = k
19
	El paralelogramo ABCD tiene de vértices A(-1,1), B(0,-1) y C(3,2). Hallar las coordenadas de D.
20
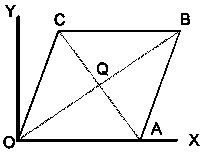	En el paralelogramo de la Fig.1: A(8,0) y Q(6,2). Calcular los otros vértices, la ecuación de las diagonales, su longitud, ángulo que forman y también el área del paralelogramo.
21
	Un paralelogramo ABCD tiene vértices en los puntos A(2,0), B(0,3) y C(-3,-3). Determinar el vértice D y el punto de corte de sus diagonales.
22
	Determinar la ecuación de una recta r de estas características: r es perpendicular a la recta que pasa por A(8,0) y B(0,5); r tiene un punto común con las rectas .. 4x-3y+1=0 y 2x+y-7=0.
23
	Sea ABCD un rectángulo de base \|AB\| =2 y altura \|AD\| =1. Sea M el punto medio del lado CD. Indíquese el valor de los siguientes productos escalares: AB·AM , AB·(AB+AM) , AB·(AC+AM).
24
	Los puntos A(2,0), B(6,0) y C(3,6) forman un triángulo. Se pide: A. Las ecuaciones de las rectas definidas por las medianas y las longitudes de estas últimas. B. Comprobar que las tres rectas anteriores son concurrentes en un punto G, y que G divide a cada mediana en dos partes tales que una de ellas es el doble de la otra.
25
	La ecuación de la recta perpendicular a 2x-4y+8=0 y que pase por el punto de intersección de las rectas: x+3y-4=0 y 2x-3y+1=0
26
	Hallar el punto simétrico A' del punto A(4,-2) respecto de la recta 2x-y-1=0.
27
	Hallar el punto simétrico A' del punto A(3,2) respecto de la recta 2x+y-12=0.
28
	¿Qué ángulo forman las rectas r y s de ecuaciones respectivas: x- 3·y+2=0 y 3·x-y+4=0
29
	El segmento definido por los puntos A (2,3) y B (6,7) se divide en cuatro partes iguales. Determinar los tres puntos que dividen al segmento mencionado.
30
	Calcular el punto simétrico del A(1,-6) respecto de la recta 3x + 4y - 2 = 4
31
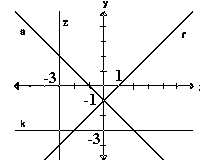	Determinar las ecuaciones de las rectas r,s,k y z de la Fig adjunta. Calcular, también, las pendientes de las mencionadas rectas y las ecuaciones del los ejes de abscisa (X) y ordenadas (Y), en todas sus formas.
32