PUNTO DE CORTE CON EJE ORDENADA (y)

Los puntos del eje y se caracterizan por tener la forma (0 , n), es decir, debemos hallar la imagen del elemento cero. Para ello se sustituye, en la función, el valor cero en la x.

(0 , n) siendo n = F(0)

Sólo puede haber, si lo hay,  un valor n, un punto de corte con el eje de ordenada.

Polinomios.

Y(x) = m·x + n               ►      (0 , Y(0))    ►    (0 , n)

P(x) = 4·x³ - 5·x + 1       ►      (0 , P(0))    ►    (0 , 1)      

G(x) = x³ - x                   ►      (0 , G(0))    ►   (0 , 0)       

Racionales.

		n(0)
	C(0) =	—————
		d(0)

con n(x) numerador y d(x) denominador.   (0 , C(0))   siempre que d(0) ≠ 0.

		x2 + 1
	C(x) =	—————	►  (0 , C(0))  ►  (0 , -1)
		x2 - 1

Exponencial.

E(x) = e^-x   ►    (0, E(0))   ►  (0 , 1).    

E(x) = e^x + e^-x      ►    (0 , E(0))    ►   (0 , 2)    

Logaritmo.

Ln (x + 2)   (log neperiano) ►  (0 , Ln(2))   ►  (0 , 0,693)   

Trigonométrica.

seno:   (0 , sen (0))  ►   (0 , 0)  

coseno:   (0 , cos (0))   ►   (0 , 1)   

tangente:   (0 , tan (0))   ►   (0 , 0)   

Como ejemplo utilicemos la función vista arriba:

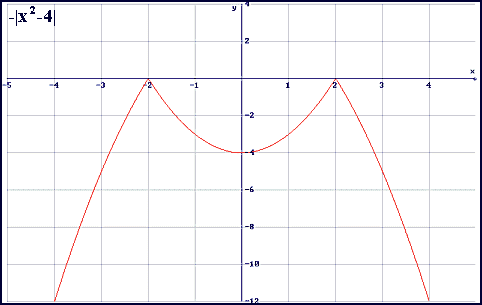
F(x) = -|x² - 4|      (donde |x| valor absoluto de x). Cortará al eje de ordenadas en:

(0 , F(0))   ►   (0 , -4)