PROBLEMAS Y CUESTIONES DE FÍSICA

DINÁMICA 1

Ir al foro de Física (Dinámica - problemas resueltos)

	Describe, en cada caso, si la aceleración es tangencial o centrípeta (radial, normal). A. Un móvil que se mueve en línea recta con v cte. B. Un móvil que se mueve en círculo con v cte. C. Un móvil que se mueve en línea recta aumentando v. D. Un móvil que se mueve en círculo disminuyendo v.
1
	Imaginemos un cuerpo de 20 kg de masa moviéndose en el espacio, lejos de cualquier otro cuerpo, en una determinada dirección. Decir si cambia de dirección o aumenta (disminuye) el módulo de su velocidad en los siguientes casos: A. Se le aplica una fuerza en la misma dirección y sentido que la velocidad. B. Se le aplica una fuerza en dirección perpendicular a v. C. Se le aplica una fuerza que forma un ángulo de 45º con v. D. Se le aplica una fuerza que se oponga al sentido de v.
2
	Si un cuerpo de masa M viajase por el espacio a una cierta velocidad y en una determinada dirección. ¿Qué dirección y sentido habría que darle a una fuerza para que el cuerpo girase en círculo? ¿Qué ocurrirá cuando dejase de actuar dicha fuerza?. Si repetimos la experiencia con un cuerpo de masa doble ¿qué habría que hacer para que girase en torno a un punto determinado?.
3
	Si empujamos un cuerpo, de masa 5 kg, con una fuerza de 10 N, durante 10 s y dejamos de empujar durante 5 s y, finalmente, le aplicamos una fuerza contraria de 2 N durante 10 s. A. Cuántos metros ha recorrido, en total, durante todo el período de tiempo. B. ¿Qué velocidad tendrá al cabo del mismo?. C. ¿Qué velocidad tenía el cuerpo para t=13 s. D. Hacer una gráfica aceleración-tiempo ; velocidad-tiempo y espacio-tiempo
4
	Si parásemos el movimiento de la Luna con respecto a la Tierra. ¿Caería la Luna sobre la Tierra? A. Si la Tierra tira de la Luna con una fuerza enorme, ¿por qué ésta no se viene hacia aquella y chocan?
5
	Si vas a comprar un Newton de jamón ¿cuántos gramos te dan?.       Un cuerpo de 1 kg ¿Cuánto pesa (en N)?       ¿Qué es un kilopondio?
6
	Demuestra por análisis dimensional que:  [a]=[m/s²]=[N/kg]
7
	Un camión deslizándose por el suelo (sin rozamiento) y con el motor apagado, choca contra una palmera y la destroza. ¿Es posible decir que la velocidad del camión es cte, antes de chocar, porque la resultante de las fuerza que actúan sobre él era cero? ¿Entonces qué destroza a la palmera?.
8
	Partiendo de la segunda ley de Newton,  explicar, con la mayor claridad posible, ¿por qué todos los cuerpos caen con la misma aceleración, independientemente de su masa?.
9
	¿Puede ser curva la trayectoria de un móvil si sobre él no actúa ninguna fuerza?. Razona la respuesta.
10
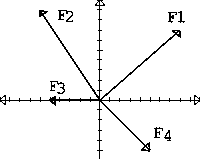	Encontrar la resultante de las fuerzas representadas en la Fig. adjunta. Si todas esas fuerzas actuaran sobre un cuerpo de masa 10 Kg, y suponiendo que partiera del reposo. ¿Qué velocidad tendría al cabo de 10 s?. ¿Qué ángulo formará la velocidad con el eje X?. ¿En qué dirección se mueve el objeto?.
11
	¿Qué significa que el coeficiente de rozamiento del acero-acero es de 0,1?.
12
	Un automóvil marcha a 72 km/h. ¿Qué aceleración negativa es preciso comunicarle para que se detenga en 100 m?. ¿Cuánto tiempo tardará en parar?. Si su masa es de 1.500 kg ¿cuál será la fuerza de frenado?.
13
	Explica de una manera clara y concisa, basando tu razonamiento en la ley de Newton, por qué todos los cuerpos aceleran lo mismo (caída libre), independientemente de su masa.
14
	Un cuerpo de 10 Kg se mueve sobre un plano horizontal al actuar sobre él una fuerza constante de 200 N paralela al plano. El coeficiente de rozamiento es de 0,1. Halla la aceleración. ¿Qué valor tendría una fuerza que sustituyera a las dos que actúan?.
15
	Calcular la fuerza que es preciso aplicar a un trineo sobre hielo, de peso 1000 N, para que cada segundo, aumente su velocidad en 10 m/s²
16
	Para bajar un cuerpo nos ayudamos de una cuerda con la que sujetamos el cuerpo. Con la fricción entre nuestra mano y la cuerda logramos aplicar una fuerza, mediante la cuerda, sobre el cuerpo. Esta fuerza dirigida hacia arriba la podemos aumentar o disminuir, aumentando o disminuyendo la presión que ejerceremos con nuestras manos en la cuerda. Calcular la aceleración con que cae un cuerpo cuando: A. La fuerza aplicada es igual al peso. B. La fuerza aplicada es la mitad que el peso. C. La fuerza aplicada es cero.
17
	Un automóvil que se mueve a 72 km/h se detiene después de recorrer 200 m; su frenado es uniforme. La masa del mismo es de 500 kg. Calcula la fuerza de frenado y el tiempo que tardó en pararse.[500 N][20 s]
18
	Un disco de siete cm de diámetro y dos de altura se encuentra situado sobre hielo. El coeficiente de rozamiento entre el hielo y el cuerpo es de 0,25 10-3. Calcular la distancia y el tiempo para pararse si el cuerpo sale a 1 m/s del bastón de un jugador. ¿Con qué fuerza debemos empujar el disco con el bastón para que  no pierda velocidad?.
19
	Un automóvil pasa de 10 m/s a 60 m/s de velocidad en 10 s; su masa es de 1.000 kg. Calcula la aceleración imprimida por las ruedas al vehículo. [5.000 N]
20
	Un cuerpo se sitúa sobre un plano inclinado 30º .Éste, se encuentra a una altura de 1 m sobre el suelo y el coeficiente de rozamiento entre el cuerpo y la superficie vale 0,20. Calcular: A. ¿Cuánto vale la fuerza normal?. B. ¿  "     "    "   "    de rozamiento?. C. ¿  "     "    "   "    resultante paralela al plano?. D. ¿  "     "    "   "    resultante perpendicular al plano?. E. ¿  "     "    " velocidad al final del plano?. F. ¿Cuánto tiempo tardará?.
21
	Sobre un cuerpo aplicamos cuatro fuerzas: F1= 10 N,  formando un ángulo de  30º  con la horizontal; F2= 15 N, formando un ángulo  de 90º con la anterior; F3= 20 N, el dirección vertical; F4= 20 N, formando un ángulo de 180º con F2. Calcular la fuerza resultante en las direcciones horizontal y vertical. La aceleración del movimiento en esas mismas direcciones. La distancia y velocidad a la que se encontrará dicho cuerpo 10 s después de aplicadas las fuerzas. Si en ese momento quisiéramos que el movimiento fuese uniforme, ¿Qué fuerza tendríamos que aplicar al cuerpo?. Masa del cuerpo 1 Kg.
22
	Un cuerpo de 50 Kg de masa se desliza por un plano horizontal a 10 m/s. En ese momento se le aplica una fuerza de 750 N. El coeficiente de rozamiento entre el cuerpo y la superficie es de 0,5. Calcular: A. La resultante de las fuerzas. [500 N] B. La fuerza de rozamiento. [250 N] C. La velocidad que posee al cabo de 10 s. [110 m/s] D. El espacio recorrido. [600 m] E. El impulso mecánico total en ese tiempo. [5.000 N·s] F. La variación de la cantidad de movimiento.[5.000 kg·m/s] G. La cantidad de movimiento inicial y final.[500 y 5.500] H. La variación de velocidad. [100 m/s] I. ¿De qué clase es la aceleración que adquiere?
23
	Un móvil de 20 kg está acelerando durante 10 s. Su velocidad pasa de 10 a 110 m/s. ¿Cuánto vale el impulso mecánico?[2000 N·s] ¿Cuál es el cambio de la cantidad de movimiento?[2000 kg·m/s]¿Cuánto vale la cantidad de movimiento final?[2.200 kg·m/s]
24
	Sobre un cuerpo de 10 Kg, que parte del reposo, actúan dos fuerzas, una de 20 N hacia la derecha (+) y otra de 5 N hacia la izquierda (-). Calcula: A. La aceleración tangencial y radial. [1,5 m/s²]. B. La velocidad después de 4 s. [6 m/s²]. C. El espacio recorrido y el sentido en ese tiempo.[12 m].
25
	Sobre un cuerpo, en reposo, de masa 5 kg, actúa una fuerza de 20 N. Calcular:   A. La aceleración del movimiento. [4 m/s²].   B. La velocidad al cabo de 7 s. [28 m/s]   C. El espacio recorrido en ese tiempo. [98 m].   D. La aceleración es tangencial o radial.
26
	Sobre un globo actúa una fuerza hacia arriba, debida a la diferencia de densidad del gas interior con respecto al aire, de 1500 N y tiene una masa total de 100 Kg. A. ¿Asciende o desciende el globo?. B. ¿Cuánto vale la aceleración y hacia dónde? [5 m/s²]. C. ¿Cuánto habrá ascendido al cabo de 5 s? [62,5 m]. D. Si el mencionado globo se despoja de 50 kg. ¿Con qué aceleración se mueve ahora? [20 m/s²].
27
	Un ascensor de 500 Kg sube con una aceleración de 2 m/s². Calcular la tensión de la cuerda. [T=6000 N]. Si el ascensor desciende con una aceleración igual a la anterior, ¿Cuánto valdría, en este caso la tensión de la cuerda? [4000 N]. Por último ¿cuánto valdría si la velocidad de subida o bajada es constante de 10 m/s?
28
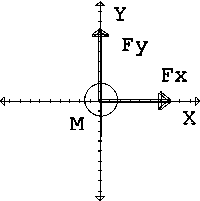	Sobre el cuerpo de la Fig, actúa dos fuerzas, una hacia la derecha, Fx, (eje X) de 20 N y otra hacia la arriba, Fy, (eje Y) de 10 N. La masa del cuerpo es de 2 kg. Calcular:   A. La aceleración que le comunicaría la Fx si actuara sola. [ax=10 m/s²].   B. La aceleración que le comunicaría la Fy si actuara sola. [ay=5 m/s² ].   C. El vector aceleración, así como su módulo y ángulo que forma con el eje X.  [a=10i+5jm/s²] ; [11,18m/s²] ; [26,56º].   D. La fuerza resultante (vector), su módulo y ángulo que forma con el eje X. [R=20i+10j N];[22,36 N];[26,56º].   E. Si multiplicamos la masa por el vector aceleración, ¿da igual que el vector fuerza?.
29
	La fuerza de rozamiento entre dos cuerpos depende de la naturaleza de la superficie de contacto de éstos (coeficiente de rozamiento, µ) y de la fuerza con se aprieten uno contra el otro (fuerza normal N; no depende de la superficie de contacto). Fr=µ·N Supongamos que un cuerpo tiene de masa 20 kg. ¿Cuánto vale la fuerza con que el cuerpo "aprieta" contra el suelo? [200 N].   A. ¿Cuánto valdría la fuerza de rozamiento o fricción si el coeficiente de rozamiento, µ, vale 0,2? [40 N].   B. ¿Qué fuerza habría de aplicársele para que se moviera con velocidad constante? [40 N]   C. ¿Qué fuerza habría de aplicársele para que acelerase 5 m/s²?   [140 N]   D. ¿Cuánto tiempo tardaría en recorrer 10 m si parte del reposo? [2 s]
30
	Un hombre de 80 Kg está colgado de una cuerda.   A. ¿Cuánto vale la tensión de la cuerda en los siguientes casos?:   B. Su velocidad es cero (reposo). [T=800 N].   C. Lo asciende con una velocidad constante de 20 m/s. [T=800 N].   D. Lo desciende con una velocidad constante de 20 m/s.[T=800 N].   E. Lo asciende con una aceleración constante de 2 m/s².[T=960 N]   F. Lo desciende con una velocidad constante de 2 m/s². [T=640 N]
31
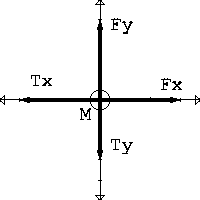	Las fuerzas de la Fig. valen: Fx=20 i N ,  Fy=10 j N.     Tx=-5 i N ,  Ty=-2 j N La masa del cuerpo es de 5 Kg.   A. ¿Cuánto vale la suma de las cuatro fuerzas? [R=(15 i + 8 j) N]   B. ¿Cuánto vale el vector aceleración? [a=3i+1,6j m/s²].   C. ¿En qué punto se encontrará el cuerpo pasados 10 s, si parte del reposo?. [r=150i+80j m]   D. ¿Cuál será el vector velocidad después de 10 s. [v=30i+16j m/s].   E. ¿Qué fuerza tendríamos que aplicarle para que el cuerpo estuviese en equilibrio (velocidad constante, o lo que es lo mismo, que a=0)? [F=-15i-8j N].
32
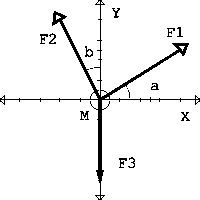	En el gráfico adjunto  hay tres fuerzas de valores: F1= 10 N  ,  F2= 100 N  ,  F3= 50 N, siendo a y b de 30º. Determinar las componentes de los tres vectores. [F1=5·31/2 i+5 j N] [F2=50 i - 50·31/2 j N] [F3=-50 j N]       Calcular el vector resultante de las tres fuerzas, así como el módulo de la aceleración. [ F=(5  3+50)i+(5-50(  3+1))j]. [|a|=14,4 m/s²].
33
	Calcular la fuerza que hay que aplicar a un cuerpo de 10 Kg, que se mueve a una velocidad de 25 m/s, para que se detenga en:    10 segundos ;   10 metros. Calcular, en ambos casos, el valor del coeficiente de rozamiento, si es ésta la fuerza  que frena al cuerpo.
34