λ : longitud de onda.     λ·f = c

 f : frecuencia.      h: cte de Plank (6,625·10^-34 J·s)

 c : velocidad de la luz (vacio; 3·10⁸ m/s)

 T : temperatura (K grados Kelvin).

 σ : cte de Stefan-Boltzmann (5,56·10^-8 wat/m²K⁴)

 Rc: radiación cavidad = ∫ R_f df = σ T⁴ .

 E = n·hf  ;  ∆E = ∆n·hf (energía emitida)

               c₁·f ⁵

 R_f = ——————

          (e ^{d·f /T} -1)    
(c₁ y d son ctes. Fórmula de Plank; fórmula empírica)

 c₁ = 2πh/c³  ;  d = h/k  (k cte Boltzmann=R/No)

   Este apartado trata de como se genera la luz y como interactúa ésta con la materia; emisión-absorción de la luz. Las fuentes luminosas más comunes son sólidos calentados y gases por los que pasa una descarga eléctrica. El filamento incandescente de una lámpara de tungsteno y el anuncio de neón son ejemplos de cada uno de estos dos tipos. Analizando la luz de una fuente con un espectrómetro, podemos averiguar con qué intensidad irradia (Rn) en cada una de las frecuencias de onda (n), en función de la temperatura (T). La figura (superior) muestra los resultados típicos de una cinta de tungsteno calentada a varias temperaturas. Para hacer este estudio se utiliza un "cuerpo negro o radiador de cavidad" (modelo) que consiste en una cavidad realizada en el interior de un material determinado. Para poder observar la radiación emitida, después de calentarlo, se realiza un pequeño orificio por el que se puede observar la radiación que se genera en el interior de la cavidad. Los hechos experimentales muestran las siguientes conclusiones:

1. La radiación en el interior de la cavidad es siempre más intensa que en el exterior.

2. Para una temperatura dada, la radiancia del agujero, Rc, es idéntica para cualquier material del que esté hecho el cuerpo radiante.

3. La radiancia de la cavidad depende de la temperatura de una manera sencilla. Rc = σ T⁴ , siendo σ una cte universal.

4. La radiación de cavidad, Rn, varía con la temperatura como muestra la figura. Estas curvas dependen sólo de la temperatura y son independiente del material, forma o tamaño de la cavidad.

   El mayor de los problemas teóricos sin resolver que existían en la física durante los últimos años del siglo pasado era la explicación de la radiación de cavidad. La física clásica (dominante) preveía la catástrofe ultravioleta. La radiancia debía aumentar indefinidamente al aumentar la frecuencia y eso no es lo que sucede. Ésta tiende a cero antes y después de un máximo de intensidad. Este máximo se va desplazando a medida que cambiamos la temperatura y se hace cada vez mayor. Para explicar estos hechos Max Plank (1.900) introdujo una serie de cambios en la forma de ver la radiación que explico de una forma precisa este fenómeno. Estos fueron:

1. Suponer que los átomos que componen las paredes se comportan como diminutos osciladores electromagnéticos. Éstos emiten y absorben energía electromagnética.

2. Un oscilador no puede tener cualquier energía sino sólo energías dadas por la fórmula: E = n·hf , siendo n la frecuencia del oscilador, h una cte (Plank) y n un número (cuántico) que toma valores enteros.

3. Los osciladores no irradian energía continuamente, sino sólo a saltos o "cuantos de energía". Estos cuantos son emitidos cuando un oscilador cambia de un estado de energía cuantizada a otro (∆E = ∆n·hf). Para  un cambio de n de una unidad la E = hf .Esta hipótesis era radical ya que la física clásica suponía de los átomos irradiaban o absorbían energía de forma continua y no a saltos o paquetes de energía (cuantos).

 W_o : energía de extracción (trabajo de extracción)

 V_f = Ec_(máx)/e = (hf - W_o)/e (potencial de interrupción)

 f_o = W_o / h (frecuencia umbral)

              hf = W_o + Ec_(máx)

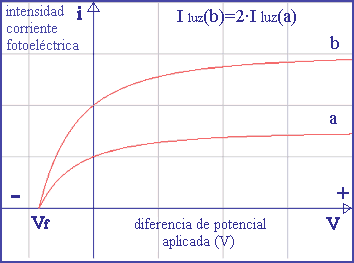
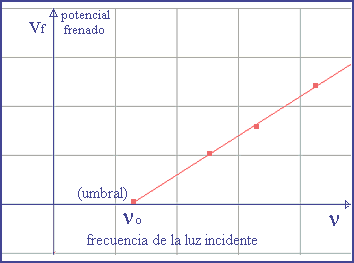
   El efecto fotoeléctrico consiste en la emisión de electrones (fotoelectrones) por un metal al hacer incidir luz  sobre él.   Este fenómeno tiene ciertas peculiaridades que no podía explicar la física clásica. En la figura superior se representa un esquema de un aparato que nos permite estudiar dicho efecto. Consiste en dos placas separadas y a las que se le somete a una diferencia de potencial mediante el uso de un divisor de tensión (podemos cambiar esta diferencia de potencial, e incluso hacerla negativa). Se coloca un galvanómetro para poder medir el paso de la corriente fotoeléctrica (i).

   Una luz monocromática que llega a la placa metálica A, pone en libertad fotoelectrones, que pueden detectarse en forma de una corriente si son atraídos a la placa metálica B. Esta corriente es medida por el galvanómetro G. En la figura inferior izquierda podemos ver esta corriente en función de la diferencia de potencial entre las placas. Se observa que aunque invirtamos la polaridad del potencial (+ en placa A y - en B) la corriente no cesa inmediatamente, a pesar de que los fotoelectrones deben moverse contra la acción del campo eléctrico creado entre las placas. Si aumentamos dicho potencial (invertido) llegamos a un valor (V_f , potencial de frenado o de interrupción) para el que la corriente cesa. Cuando el potencial es positivo (- en placa A y + en B), observamos que al aumentar la intensidad de la fuente luminosa (más luz) también aumenta la corriente, alcanzando un valor límite para valores grandes de la intensidad luminosa. Es decir, sobrepasado un cierto valor de esta intensidad de luz, la intensidad de la corriente fotoeléctrica no cambia, alcanzando un valor límite. También se ve que para intensidades de luz mayores (I_luz b>I_luz a) la corriente eléctrica es mayor pero el potencial de frenado es el mismo (independientemente de ésta). En la figura inferior derecha puede verse que dicho potencial de frenado sí depende de la frecuencia de la luz incidente, aumentando al aumentar ésta. La luz con mayor frecuencia tiene más energía. Si multiplicamos la carga del electrón por el potencial de frenado obtenemos la energía potencial eléctrica de éstos. Si esta energía se iguala a la cinética se interrumpe la corriente, por tanto: e·V_f = Ec_(máx).

Hay tres características del efecto fotoeléctrico que no se podían explicar mediante la teoría ondulatoria de la luz:

1. La teoría ondulatoria requiere que la energía cinética de los fotoelectrones aumente conforme el rayo de luz se haga más intenso. Como hemos dicho esto no ocurre ya que Ec_(máx) (=e·V_f ) es independiente de la intensidad de la iluminación.

2. De acuerdo con la teoría ondulatoria, el efecto fotoeléctrico debería ocurrir para cualquier frecuencia de la luz, con la única condición de que la luz sea suficientemente intensa. Pero la figura inferior derecha pone de manifiesto que hay una frecuencia (llamada umbral) por debajo de la cual no ocurre el efecto en cuestión.

3. Si la luz fuese suficientemente débil deberíamos esperar un retardo en el tiempo de emisión (incluso para frecuencias altas de ésta). El efecto fotoeléctrico ocurre instantáneamente. No hay retardo, independientemente de la intensidad lumínica.

   Einstein logró explicar el efecto fotoeléctrico haciendo una hipótesis notable, a saber, que la energía de un haz de luz avanzaba por el espacio en haces concentrados, llamados fotones. La energía E de un sólo fotón se expresa mediante la fórmula E = hf .Recordemos que Plank creía que la luz, aun cuando emitida por su fuente en forma discontinua, avanzaba por el espacio en forma de ondas electromagnéticas. La hipótesis de Einstein suguiere que la luz, al avanzar por el espacio no se comportaba como onda sino como partícula. Aplicando un simple principio de conservación de energía a los fotoelectrones dedujo que:    hf = W_o + Ec_(máx). Es decir, la energía de los fotones (hf) se utiliza para escapar del metal (trabajo de extracción, Wo) y lo que le sobra es energía cinética. Esto explica todas las contradicciones que había entre este fenómeno y la física clásica, a saber:

1. En lo referente al punto 1 ( el hecho de que Ec_(máx) no dependa de la intensidad de la luz) , hay una concordancia completa entre la teoría de fotón y la experiencia. El duplicar la intensidad luminosa simplemente duplica el número de fotones, y en esta forma duplica la corriente fotoelectrónica; no cambia la energía (h·f) de los fotones individuales.

2. En la objeción 2 ( la existencia de frecuencia de corte) se deduce de la ecuacion (hf = Wo + Ec_(máx)) que si Ec(máx) es cero entonces hf_o = W_o. Esto establece que el fotón tiene apenas enegía para saltar del metal y no le queda energía cinética. Por debajo de una cierta frecuencia (f_o) el electrón no tiene suficiente energía para ser arrancado del metal.

3. La objeción 3 (no hay tiempo de retardo) se deduce de la teoría fotónica, porque la energía requerida es porporcionada en un haz concentrado. No se distribuye uniformemente en una área extensa, como en el caso de la teoría ondulatoria.

      h² ε_o

 r = ——— n²    con  n = 1, 2, 3, ...

      πme² 

( ε_o cte dieléctrica)

            me⁴

 E = -  ———— · (1/n²)    con n = 1, 2, 3, ...

           8πε_o h² 

         me⁴                   

 f = ————    [(1/n²) - (1/m²)]

       8ε_o²h³                 

  f = (e²/4πε_o mr)^1/2  ;    p = mv     ;  L = r · p

 f_o = V/2πr  (frecuencia de rotación)

  L = n·h/2π    (h/2π  hache con barra)

   Ernest Rutherford propuso un modelo del átomo que se asemejaba a un pequeño sistema planetario. Esto fue consecuencia de los experimentos de dispersión de partículas a en el experimento realizado por Hans Geiger y Ernest Marsden. En este experimento se lanzaban partículas cargadas positivamente y de bastante masa contra una delgada lámina de oro; casi todas las partículas se desviaban poco o no nada pero algunas de ellas rebotaban en la dirección de la que provenían. Supuso, entonces, que el núcleo de este sistema planetario eléctrico estaba constituido por una gran masa de carga positiva y de pequeño volumen (protón). A su alrededor giraba una carga de igual, negativa, pero de mucha menor masa (electrón). El volumen atómico era grande pues el electrón giraba bastante alejado del núcleo y su masa era aportado por éste. Este modelo contradecía claramente a la física clásica pues se sabía que toda carga acelerada (toda partícula que gira tiene aceleración centrípeta o radial) debía emitir energía y por tanto el electrón, al ir perdiendo ésta de forma continua para convertirla en radiación, tendría órbitas cada vez más próximas al núcleo, estrellándose contra él. Además, el estudio espectroscópico de radiación mostraba que las emisiones eran discontinuas, mostrando rayas en algunas longitudes de onda pero no en un espectro continuo (su modelo no explicaban las rayas espectrales).  Propuso un modelo que estaba dentro de la física predominante pero esa misma física fue la tumba del modelo. Niels Bohr, en 1913,  propuso tres postulados (revolucionarios) que sí podrían explicar el espectro del átomo de hidrógeno:

1.    Los electrones giran en órbitas circulares (modelo de Rutherford) alrededor del núcleo pero sin emitir energía radiante (estado estacionario).

2.    Al igual que Plank propuso que no eran posibles todas la frecuencia de emisión de luz (cuerpo negro) sino sólo múltiplos de ésta, Bohr propuso que no era posible cualquier órbita sino sólo las que cumplían una condición; su momento cinético tenía que ser múltiplo entero de la cte de Plank dividido por 2p (hache con barra). Esta cte tiene dimensiones (y por tanto unidades) de momento cinético. Es decir:  L = I·w = n ·h/(2π)

3.    Los átomos irradiarían sólo en el caso de cambiar de órbita (cambio entre estados estacionarios permitidos de energía E_n). Aplicó los descubrimientos de Plank y dedujo que esa energía debía ser: E_n - E_k = hf, siendo hf  el quantum de energía que se lleva el fotón emitido por el átomo durante la transición.

   Para averiguar las frecuencias posibles (hf) es necesario conocer las energías de los diversos estados estacionarios en los cuales puede existir un átomo de hidrógeno. Este cálculo fue efectuado por primera vez por Bohr, fundándose en un modelo específico del átomo de hidrógeno propuesto por él. Este modelo tuvo un gran éxito y contribuyó a la creación de la mecánica cuántica; una nueva y revolucionaria forma de entender el mundo.

   Supongamos que el electrón (con carga e y masa m) en el átomo de hidrógeno se mueve en una órbita circular de radio r con centro en su núcleo. Supongamos que el núcleo, que es un simple protón, es de masa tan grande que el centro de masas del sistema se encuentra donde está el protón. Calculemos la energía de este átomo. Apliquemos F = m· a_c , donde F es la fuerza eléctrica (ley de Culomb; F = K·q·q'/r² , con K = 1/ 4πε_o = 9·10⁹ en el vació ) y  a_c es la aceleración centrípeta (v²/r). Así pues: 

   Ya que el radio de la órbita puede tomar cualquier valor, también puede tomarlo la energía E. El problema de cuantizar la energía se reduce a cuantizar el radio. Como L = I·w = r·mv (en una órbita circular) y esta magnitud está cuantizada (por el segundo postulado) deducimos que:

(n, número cuántico; radios de órbitas permitidas). Sustituyendo en E tenemos:

  Por último, como  E = h·f  entonces despejando f tenemos:

   Esta ecuación explicaba bastante bien las líneas espectrales del átomo de hidrógeno y es por ello, que aunque con suposiciones atrevidas e incluso arriesgadas, esta teoría fue aceptada.

   Cuando un electrón recibe energía externa (luz, calor, etc) salta a estados excitados de energía (n mayores), al cabo de un tiempo vuelve a su estado inicial (n menos) emitiendo un fotón de energía E y por tanto de una frecuencia definida por las ecuaciones anteriores. Cada una de estas frecuencias, tomadas para distintos valores de m y n se llaman series (Liman, Paschen, etc). Ver gráfico superior.

Bibliografía: Halliday-Resnick