|
|
|
CAMPO ELÉCTRICO |
||
| Ley de Coulomb |
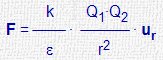 |
ε : cte dieléctrica relativa (al vacio) ur = r / |r| vector unitario radial k = 9·109 (en el vacio) (S.I.) |
| Fuerzas que un sistema de cargas puntuales (Qi)ejerce sobre otra carga puntual (Q) |
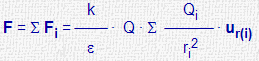 |
ri = vector de Qi a Q ≠ 0 ur(i) = vector unitario de Qi a Q |
| Fuerza ejercida por una distribución continua de cargas |
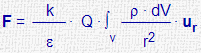 |
ρ = densidad de carga V: volumen |
| Teorema de Gauss |
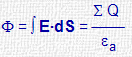 |
Φ : flujo campo eléctrico εa = ε · εo (cte dieléctrica absoluta) |
|
INTENSIDAD CAMPO ELÉCTRICO |
POTENCIAL ELÉCTRICO |
|
| Carga aislada |
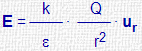 |
|
| Sistema de cargas |
 |
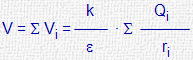 |
| Distribución continua de cargas |
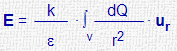 |
|
| Esfera conductora cargada de radio R | ||
| En el interior (r<R) | E = 0 |
|
| En la superficie (r=R) |
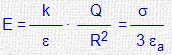 |
|
| En el exterior (r>R) |
 |
 |
| Esfera dieléctrica cargada de radio R | ||
| En el interior (r<R) |
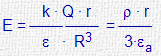 |
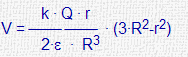 |
| En la superficie (r=R) |
 |
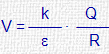 |
| En el exterior (r>R) |
|
|
| Campo creado por un hilo conductor cargado de longitud infinita a una distancia r |
E = k·λ /(ε·r) |
λ: densidad lineal de carga (Q/long) |
| Campo creado por un plano infinito cargado uniformemente |
E = σ/(2·εa) |
σ: densidad superficial de carga (Q/Sup) |
| Campo creado en un punto infinitamente próximo a la superficie de un conductor |
E = σ/εa |
|
| Energía potencial eléctrica de un sistema | ||
| Dos cargas |
|
|
| n cargas |
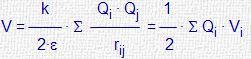 |
con i ≠ j i,j : 1....n |
| Relación entre el campo y el potencial |
E = - grad V E = - dV/dr |
V = - ∫ E · dr |
|
CAPACIDAD ELÉCTRICA |
||
| Polarización | P = n·p
P = σi P = κ·εo·E |
P: polarización (momento dipolar por unidad de volumen) n: número de moléculas por unidad de volumen p: momento deipolar de una molecula. σi: densidad superficial de carga inducida en el dieléctrico κ: suceptibilidad eléctrica |
| Equivalencias |
ε = 1+κ = εa/εo εa = ε·εo = ε·(1+κ) |
κ = ε - 1= (εa -εo )/εo |
|
Desplazamiento elétrico o inducción electrica |
D = εo·E + P = εa·E D = σ |
σ: densidad superficial de carga libre en el conductor. E: campo eléctrico |
| Capacidad de un conductor | C = Q/V |
Q: carga V: potencial |
| Capacidad de una esfera conductora cargada de radio R | C = 4πε·εo·R | |
| Energía de un condensador cargado | E = Q2/(2C) = C·V2/2 = Q·V/2 | |
|
CONDENSADORES |
||
| Capacidad de un condensador | C = Q/∆V | ∆V: diferencia de potencial entre sus armaduras |
| Condensador plano | C = εa·S/d |
S: superficie de las armaduras d: separación entre láminas |
| Condensador esférico | C = 4πεoR1·R2 / (R2-R1) |
R2: radio exterior R1: radio interior h: longitud |
| Condensador cilíndrico | C = 2πεa·h / Ln(R2/R1) | |
| Carga de un condensador en una resistencia |
q(t) = Q·(1 - e -t/RC) i(t) = I· e -t/RC |
ζ = R·C : constante de tiempo R: resistencia |
| Descarga de un condensador en una resistencia |
q(t) = Q· e -t/RC i(t) = -I· e -t/RC |
|
| Energía de un condensador cargado | Ep = Q2/(2C) = CV2/2 = Q·V/2 | Ep: energía potencial |
| Densidad de enegía electrostática | u = εa·E2/2 = D·E / 2 | |
| ASOCIACIÓN DE CONDENSADORES | ||
| Paralelo | V = Vi ; Q = ∑Qi ; C = ∑Ci | |
| Serie | V = ∑Vi ; Q = Qi ; (1/C)=∑ (1/Ci) | |